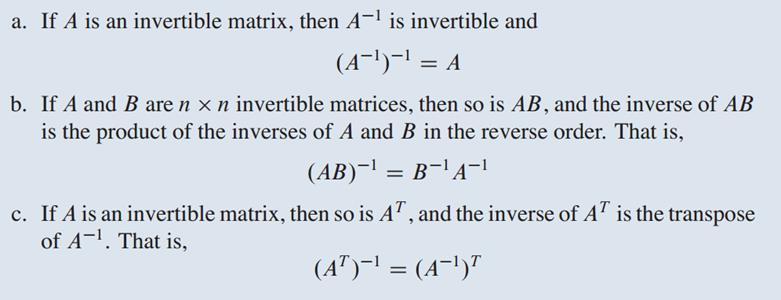linear algebra - If A is invertible, then it can be represented as a product of elementary matrices. - Mathematics Stack Exchange

2 - 1 Chapter 2A Matrices 2A.1 Definition, and Operations of Matrices: 1 Sums and Scalar Products; 2 Matrix Multiplication 2A.2 Properties of Matrix Operations; - ppt download

SOLVED: Express the invertible matrix 1 2 1 1 0 1 1 1 2 A = as product of elementary matrices. Use this to express A-1 as product of elementary matrices

linear algebra - Why is a matrix invertible if it can be written as the product of elementary matrices? - Mathematics Stack Exchange

linear algebra - Why is the product of elementary matrices necessarily invertible? - Mathematics Stack Exchange

linear algebra - Why can all invertible matrices be row reduced to the identity matrix? - Mathematics Stack Exchange
![Suppose [math]A,B[/math] are [math]n\times n[/math] matrices such that [math]AB[/math] is invertible and [math]B[/math] is invertible. How do you prove that [math]A[/math] is invertible? - Quora Suppose [math]A,B[/math] are [math]n\times n[/math] matrices such that [math]AB[/math] is invertible and [math]B[/math] is invertible. How do you prove that [math]A[/math] is invertible? - Quora](https://qph.cf2.quoracdn.net/main-qimg-da6ca456a38e948908176db1128d33ea.webp)
Suppose [math]A,B[/math] are [math]n\times n[/math] matrices such that [math]AB[/math] is invertible and [math]B[/math] is invertible. How do you prove that [math]A[/math] is invertible? - Quora



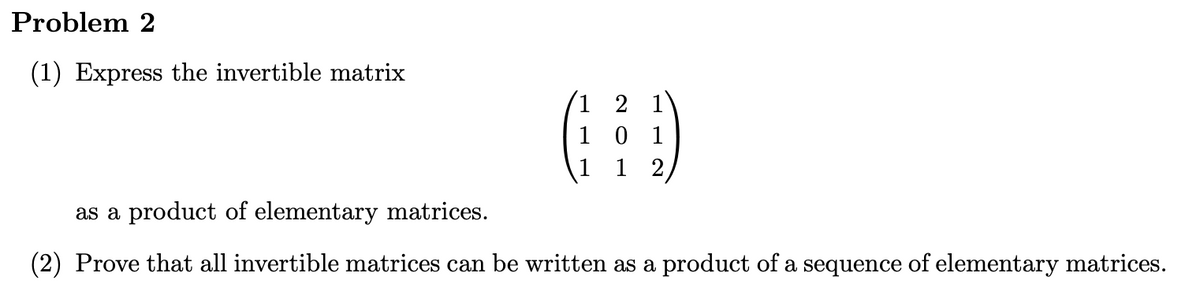



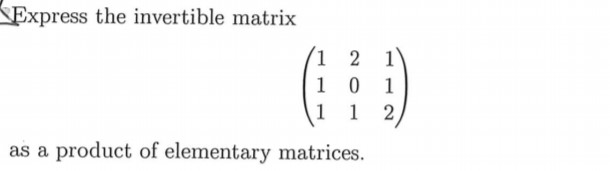

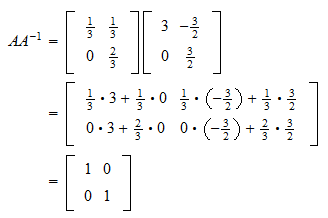
![ANSWERED] Express the following invertible matrix A as a produ... - Algebra ANSWERED] Express the following invertible matrix A as a produ... - Algebra](https://media.kunduz.com/media/sug-question-candidate/20230207145904558623-5366860.jpg)